https://www.acmicpc.net/problem/15649
15649번: N과 M (1)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
백준에서 이 문제를 풀면서 백트래킹에 대해 학습을 하였다.
분명 이전에 공부했던 내용이지만, 코드로 구현하는 방법이 떠오르질 않았다.
그래서 이번에 공부하면서 알았던 것들을 정리해 보고자한다.
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
void printArr(vector<int>& choose, vector<bool>& visited, int stack, int num) {
if (stack == num) {
for (int & i : choose) {
cout << i << ' ';
}
cout << '\n';
}
else {
for (int i = 0; i < num; i++) {
if (visited[i] == true)
continue;
else {
visited[i] = true;
choose[stack] = i + 1;
printArr(choose, visited, stack + 1, num);
visited[i] = false;
}
}
}
}
int main() {
int num;
cin >> num;
vector<bool>visited;
vector<int>choose;
visited.resize(num);
choose.resize(num);
for (int i = 0; i < num; i++) {
visited[i] = false;
choose[i] = 0;
}
printArr(choose, visited, 0, num);
return 0;
}
인터넷에 나오는 정답 코드들을 토대로 다시 만든 코드 이다.
백트래킹이나 dfs 모두 재귀를 통해 구현하기 때문에 왜 이 코드가 모든 경우의 수를 출력 해주는지 이해하기가 힘들었다. 재귀는 구현하기 까다로운 것을 쉽게 구현할 수 있게 해주지만, 작성자 이외의 사람이 보기에는 이해가 힘들 수도 있다는 단점이 있다.

예를 들어 4이하의 숫자로 만들 수 있는 길이 4의 모든 수열을 출력 하고자 하는 경우, 4! = 24 가지가 존재 한다.
우선 재귀를 통해 [1, 2, 3, 4]라는 첫 번째 경우의 수를 구합니다. 결과 출력후 return을 통해 함수가 종료. 이후 4번째 숫자를 선택하기 전으로(TTTF) 돌아갑니다. for 반복문에 의해 i의 값이 증가, i < num 을 만족시키지 못하므로 반복문이 종료. 3번째 숫자를 선택하기 전(TTFF)로 돌아간다. i = 2 이므로, i의 값이 증가하여 3이 되어도 num = 4 보다 작기 때문에 반복문이 실행 된다. 이때, stack = 2 i = 3 이므로, 세번째 원소로 4가 입력되게 된다.
이번에 백트래킹을 학습하면서 문득, dfs랑 다른 점이 뭘까 라는 생각이 들었다.
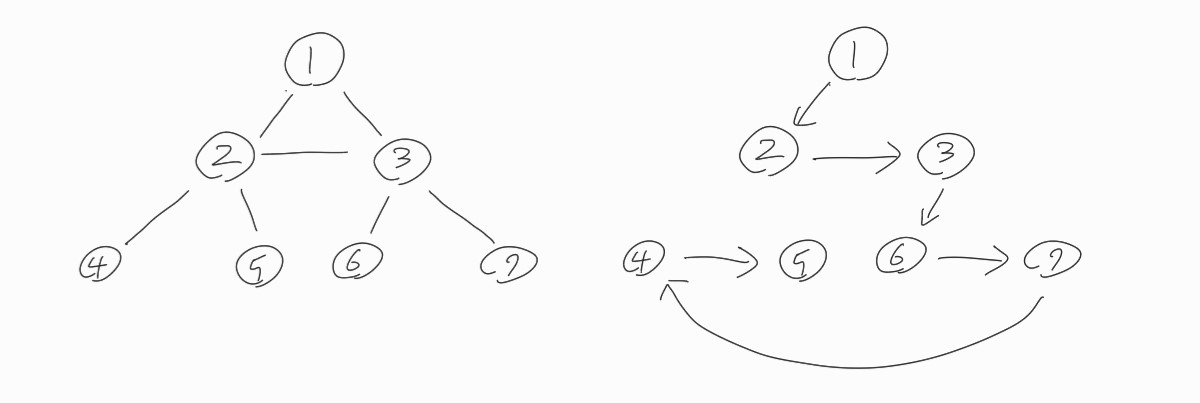
dfs는 이와 같은 그래프가 있다고 할때, 방문하지 않은 인접한 노드가 없을 때까지 파고 들어가 탐색하는 기법이다. dfs또한 스택의 구조 이기에 재귀를 이용하여 구현한다.
유튜브를 돌아다니다가 이 영상을보고 차이점을 깨달았다.
https://www.youtube.com/watch?v=atTzqxbt4DM&t=312s
이 영상이 백트래킹과 dfs의 차이에 대해 설명해주지는 않지만, 3분 38초 즈음, 재귀 함수 구성에 대한 설명에서 백트래킹은 재귀 함수의 반환(종료) 조건으로 깊이를 설정하지만, dfs는 해당 노드를 방문 했는지로 반환 여부를 결정한다.
사실 간단한 문제 였습니다. dfs는 최단 경로를 구하기위해 가장 먼저 구해지는 한 가지를 출력하고 종료하지만, 백트래킹은 조건을 만족하는 모든 경우를 구하기 위해 사용하기 때문에 재귀 함수의 구성이 유사 하더라도 반환(종료) 조건에서 명확한 차이가 있었던 것이다.
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [알고리즘 정리] - 동적 계획법(Dynamic Programming) (0) | 2024.03.02 |
|---|---|
| [알고리즘 정리] - Kruskal 알고리즘 (0) | 2023.08.28 |
| [알고리즘 정리] - DFS(Deprth First Search), BFS(Breadth First Search) (0) | 2023.08.04 |

