[프로그래머스/C++] - 등굣길
https://school.programmers.co.kr/learn/courses/30/lessons/42898
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
프로그래머스에서 코테 준비를 하다가 만난 문제이다. 특별히 유별나게 어려운 문제는 아니었지만 코드 작성에 어려움을 많이 겪었기에 한 번 정리해보려 한다.

문제는 단순하다 집이 있는 좌표를 (1, 1)이라고 할 때, (n, m)지점에 있는 학교까지 갈 수 있는 최단 경로의 수를 구하는 것이다.
문제를 읽고 최초로 시도한 것은 DFS였다. 사실 시간 초과가 날 것같은 불안감에 코드를 작성하면서도 자신이 없었는데, 실제로 돌려보니까 시간초과가 났다.
그러다 이 문제의 카테고리가 dp인 것을 확인하고 어떻게 dp를 사용할지 고민하던 중, 이전에 백준에서 풀었던 문제가 떠올랐다.
https://www.acmicpc.net/problem/1520
1520번: 내리막 길
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으
www.acmicpc.net
이 문제는 다음 좌표가 현재 좌표의 수보다 낮은 지점으로만 이동할 수 있는 문제로 이번 글에서 다루고 있는 '등굣길'과는 좀 상황이 다르기는 하나, 문제를 푸는 핵심 알고리즘은 같다. DFS + DP를 동시에 사용하는 것이다.
그렇다면 DFS + DP를 활용한 '등굣길' 문제의 정답 코드를 보자. '내리막 길'문제의 정답 코드를 참고하여 작성한 '등굣길' 문제의 정답코드는 아래와 같이 작성하였다.
#include <string>
#include <vector>
#include <iostream>
using namespace std;
vector<vector<int>> dp(101, vector<int>(101, -1));
int adjacent[101][101];
// dp[i][j] -> n, m에서 i, j까지 오는 방법의 수
struct Pos{
int X;
int Y;
};
int N, M;
int frontX[2]{1, 0};
int frontY[2]{0, 1};
int dfs(Pos curPos) {
if (curPos.X == M && curPos.Y == N) { // 목적지 도착 시 1반환
return 1 % 1000000007;
}
if(dp[curPos.Y][curPos.X] != -1) { // 이미 방문 기록이 있다면 그것을 반환
return dp[curPos.Y][curPos.X] % 1000000007;
}
dp[curPos.Y][curPos.X] = 0; // 첫 방문 처리
for(int i = 0; i < 2; i++) {
Pos nextPos{curPos.X + frontX[i], curPos.Y + frontY[i]};
// 맵안에 존재하는 지점인가
if(nextPos.X > 0 && nextPos.X <= M && nextPos.Y > 0 && nextPos.Y <= N) {
if(adjacent[nextPos.Y][nextPos.X] == 0) { // 물웅덩이가 아닌 지점인가
if(dp[nextPos.Y][nextPos.X] != 0) { // 방문한적 없는 지점인가
dp[curPos.Y][curPos.X] += dfs(nextPos);
}
}
}
}
// 도착 못했다면 현재 지점 가짓 수 반환
return dp[curPos.Y][curPos.X] % 1000000007;
}
int solution(int m, int n, vector<vector<int>> puddles) {
int answer = 0;
N = n;
M = m;
for(int i = 0; i < puddles.size(); i++) {
adjacent[puddles[i][1]][puddles[i][0]] = 1;
}
answer = dfs(Pos{1, 1}) % 1000000007;
return answer;
}
코드만 봐선 솔직히 이해가 안된다. 그림을 통해 하나씩 정리해보자.
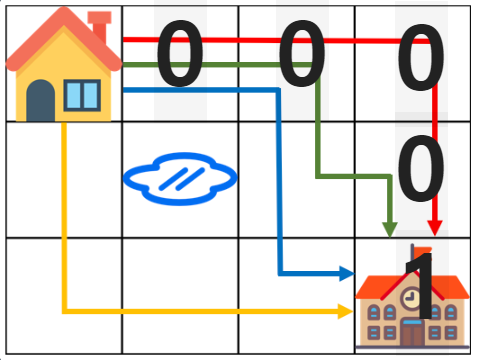
우선 최초에 위와 같은 경로를 찾고 dp배열의 값을 위와 같이 초기화 할 것이다. 위의 그림에서 0과 1이외에는 전부 -1로 설정되어있다.
위의 그림은 빨간색 경로를 찾았을 때의 시점이다. 목적지에 도착하여 1을 반환 받은 직후의 모습이다.
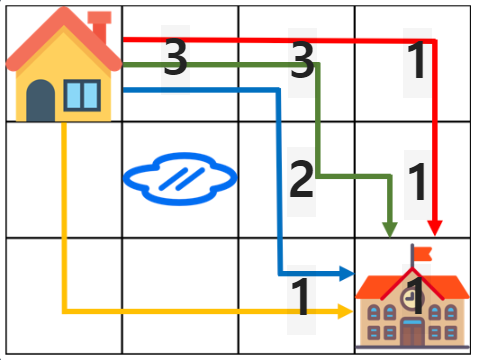
그 이후에 초록과 파랑 경로를 찾게 되면 위와 같은 상황이 된다. 그림이 좀 이상할 수 있는데, dp 배열의 개념을 아래와 같이 생각하는 것이 좋다.
'dp[i][j] -> n, m부터 i, j까지 오는 방법의 수'
문제에서 원하는 것은 1, 1에서 n, m까지의 방법의 수인데 왜 거꾸로 하냐는 의문이 들 수도 있지만 이것이 memoization 기법이기 때문에 그렇다. 그리고 집에서 학교로 가는 방법이나 학교에서 집으로 가는 방법이나 같기 때문에 이 부분은 논란의 여지가 없을 것이다.
다시 그림으로 돌아와서, 집에서 오른쪽으로 갈때 학교까지 도달하는 방법은 빨강, 초록, 파랑의 3가지 이므로 dp배열에는 위와 같은 값들이 들어간다.
그 뒤로는 똑같다. 아래로 가는 경로의 수도 체크하여 최종적으로는 dp[1][1](혹은 dp[0][0] 시작 지점을 어디로 설정하느냐에 따라)을 반환 하면 그것이 n, m까지 도달하는 최단 경로의 수가 될 것이다.
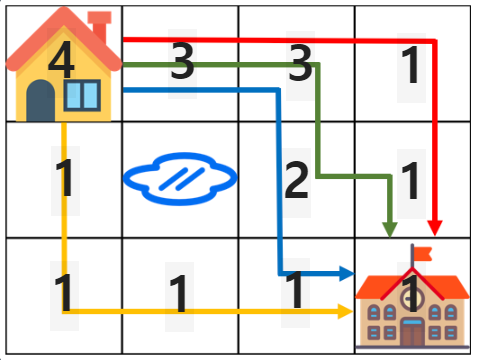
DFS완료 후에는 최종적으로 위와 같은 상태가 된다. 즉 집에서 학교까지(학교에서 집까지) 가는 최단 경로의 수는 4가지 임을 구할 수 있다. 문제의 핵심은 DFS를 사용하되 DP를 통해 중복된 연산을 피하는것이다. 예를 들면 (2, 3)지점에서 (2, 4) 지점으로 이동하는 순간 (2, 4)의 값이 1이므로 굳이 학교까지 가는 연산을 더 할 것이 아니라 (2, 4)의 값인 1을 (2, 3)인 지점에 더해주는 것이다.
사실 이런식으로 DP를 이용하여 경로의 개수를 역순으로 구한다는 것은 정답 코드를 보고 분석하기 전까지 떠올리는것은 거의 불가능에 가까운것 같다. 어쨌든 최단 경로의 개수는 흔한 유형이기도 하고 자주 볼 수 있는 유형이니 이 방식에 익숙해지는 것이 좋을 듯하다.
